概要
3次元の回転行列、三次元極座標、Euler角、姿勢計算、クォータニオン、2地点間の距離、1/25000地形図の生成時の計算誤差、緯度・経度の、 10進数と60進数(度分秒)の変換、
リンク
[] 3次元の回転行列
3次元の回転行列
w3e.kanazawa-it.ac.jp
[] 三次元極座標についての基本的な知識 | 高校数学の美しい物語
三次元極座標についての基本的な知識 | 高校数学の美しい物語
三次元極座標の基本的な知識（意味，変換式，逆変換，重積分の変換など）とその導出を解説。
manabitimes.jp
[] 【姿勢計算】Euler角と回転行列 #Rotation – Qiita
【姿勢計算】Euler角と回転行列 - Qiita
はじめに回転計算について、何度も調べては実装を繰り返しています。今回もまた調べて実装したので、メモっておきます。姿勢計算は、自動運転やロボティクスでは必ず使われます。3つの軸xyz の正規直行系…
qiita.com
[] 姿勢の算出 | 株式会社スポーツセンシング
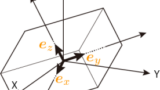
姿勢の算出 | 株式会社スポーツセンシング
モーションセンサのジャイロセンサは角速度（回転の速度）を計測するので，姿勢角度を直接算出できません．また，地磁気センサの情報からは3次元の角度のうち2つの角度しか計算することができません．そこで，ここではモーションセンサの計測データから姿勢角度を算出する方法についてご説明する前に，まずは3次元の角度について概要を述べま...
www.sports-sensing.com
[] ゆるめのクォータニオン入門 | NEXTSCAPE with MR
ゆるめのクォータニオン入門 | NEXTSCAPE with MR
withmr.nextscape.net
[] 回転ベクトル・回転行列・クォータニオン・オイラー角についてまとめてみた – かみのメモ
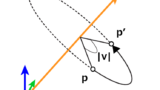
回転ベクトル・回転行列・クォータニオン・オイラー角についてまとめてみた - かみのメモ
この記事では回転ベクトル,回転行列,オイラー角,クォータニオン(四元数)それぞれについて回転の表現方法,特徴,右手系・左手系の変換方法を紹介します。
kamino.hatenablog.com
[] クォータニオン (Quaternion) を総整理！ ～ 三次元物体の回転と姿勢を鮮やかに扱う ～ #Unity – Qiita
クォータニオン (Quaternion) を総整理！ ～ 三次元物体の回転と姿勢を鮮やかに扱う ～ - Qiita
0. はじめに: クォータニオンについて思うことはじめまして！NTTデータ数理システムで機械学習やアルゴリズムといった分野のリサーチャーをしている大槻 (通称、けんちょん) です。本記事は、東…
qiita.com
[] TrailNote : 2地点間の距離の計算
TrailNote : 2地点間の距離の計算
1/25000地形図印刷・ルート編集アプリ(for Mac)
www.trail-note.net
[] TrailNote : 作成した地形図の精度の確認
TrailNote : 作成した地形図の精度の確認
1/25000地形図印刷・ルート編集アプリ(for Mac)
www.trail-note.net
[]
平成 26 年度 物理学基礎 講義資料 第9 回 極座標での運動の取り扱い −円運動、振り子の運動−
[] 2次元極座標系の運動方程式 | 高校物理の備忘録
2次元極座標系の運動方程式
平面上で回転運動を行なう物体の運動方程式を記述するのに便利な座標系である2次元極座標系について議論します.
physnotes.jp
[] 【みんなの知識 ちょっと便利帳】緯度・経度の、10進数と60進数（度分秒）の変換 – 文字だけでのシンプル変換
【みんなの知識 ちょっと便利帳】緯度・経度の、10進数と60進数（度分秒）の変換 - 文字だけでのシンプル変換
緯度・経度の、10進数と60進数（度分秒）の変...
www.benricho.org
[] 【みんなの知識 ちょっと便利帳】地図上で2地点の方角・方位、距離を調べる
【みんなの知識 ちょっと便利帳】地図上で2地点の方角・方位、距離を調べる
地図上で2地点の方角・方位を調べることができます。住所や都市名、地名、キーワードなどを入力して計測します。「○○から○○の方角は？」が調べられます。2地点の直線距離も分かります。マーカーをドラッグして移動することも出来ます。『みんなの知識 ちょっと便利帳』の一部です。
www.benricho.org
[] [Python]緯度経度から2地点間の距離と方位角を計算する #Python – Qiita
[Python]緯度経度から2地点間の距離と方位角を計算する - Qiita
##はじめにA地点とB地点の緯度経度から距離と方位角を計算する方法について調べてみました。地球は完全な球体ではなく赤道半径が6378.137km、極半径が6356.752kmで楕円体に近い形のた…
qiita.com
[]
[] ３次元における回転座標変換行列 – 理系的な戯れ
３次元における回転座標変換行列 - 理系的な戯れ
はじめに 飛行機、ミサイル、ドローン、潜水艦、それに２次元平面上を動く場合もピッチやロールの自由度がある場合など おおよそ３次元に動き回れるものの運動をモデル化するには回転運動をどう扱うかと言う話から避けては通れないと思います。 今回は、その基礎となる回転行列と座標変換行列について話をしようと思います。 探せばこの手の...
rikei-tawamure.com
コメント